 I put this story together for Plus - I'll be writing their new regular Sports Column, which will focus on maths and sport. For more maths stories on sport, see previous Plus stories tagged with sport. And for more on this particular story, see it as published in The Plus Sports Page: Power Trip
I put this story together for Plus - I'll be writing their new regular Sports Column, which will focus on maths and sport. For more maths stories on sport, see previous Plus stories tagged with sport. And for more on this particular story, see it as published in The Plus Sports Page: Power TripBeing the manager of a Premier League football club may seem like one of the most glamorous jobs in the world — with the fame comes fortune and the opportunity to travel (well, to Hull, Wigan and Portsmouth anyway). However, as far as job security goes, football managers live on the edge. Their terms can be terminated almost on a whim by their club's owner, and they live and die by their team's results.
It would seem that there is no way to predict how long their tenures will be. However, a collection of researchers from the UK, Singapore and the US have found that there may be a strong mathematical trend underlying how long football managers stay in their jobs.
Toke S. Aidt, Bernard Leong, William C. Saslaw and Daniel Sgroi found that the distribution of tenure lengths for managers of sporting teams in many countries obey power laws. Power laws are fascinating because they arise in a surprisingly large number of naturally occurring phenomena, such as the size of cities, stock market returns, cook book ingredients and even how many times certain words are used in long books.
A power law has the form
![\[ y = ax^ b, \]](http://plus.maths.org/MI/plus/latestnews/sep-dec08/managers/indexhtml1/images/img-0001.png) |
where x and y are variables and a and b are constants. The exponent b is usually negative, so y decreases as x increases. In the case of football managers, the researchers found that
![\[ n=a(t+1)^ b, \]](http://plus.maths.org/MI/plus/latestnews/sep-dec08/managers/indexhtml1/images/img-0006.png) |
To derive this formula, the authors plotted tenure lengths of real managers against their time of dismissal and then set out to find the curve that best describes the data. In fact, to make things easier, they looked at logarithms, which turn a curve of this form into the straight line
![\[ ln(n) = ln(a) + bln (t+1). \]](http://plus.maths.org/MI/plus/latestnews/sep-dec08/managers/indexhtml3/images/img-0002.png) |
For tenures greater than one year, they found that in the English Premier League, football leagues across Europe, and American football and baseball competitions, there is a straight line of this form that fits the data. Moreover, the fit is statistically significant, that is, it’s not just due to chance.
The following graph is for English Premier League managers between 1874 and 2005.
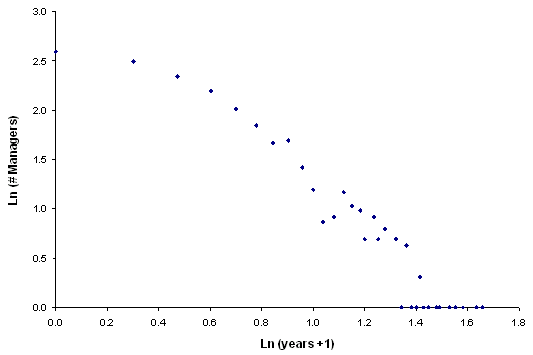
The logarithm of the length of managers' career plotted against the logarithm of the number of managers dismissed at that time of their career. The data can be approximated by a straight line and the fit is statistically significant. The data come from the English Premier League between 1874 and 2005.
But what does all this mean?
As we mentioned earlier, power laws are compelling as they can emerge from simple mathematical rules — the power law is often a macroscopic outcome of microscopic interactions between the players in the system (in this case football managers, the team, club owners and fans, etc). In fact, power laws are often seen as the signature of complexity. In the 1980s scientists found that there are dynamical systems based on simple rules which, through self-organisation, bring themselves into extremely sensitive states, where even the smallest change can cause wide-ranging and unpredictable chain reactions.
An often quoted example of this phenomenon involves a pile of sand. When you sprinkle sand on a table, a pile will build up and after a while reach a maximal slope: any additional grain of sand will cause avalanches whose number and size are impossible to predict. Such a sensitive state is called a critical state and this behaviour is called self-organised criticality. It is an interesting phenomenon, because it may explain "spontaneous" emergence of complexity in nature, which is not a result of someone forcing the system.
When a system has reached a critical state through self-organisation, it can often be described by power laws. In our sand example, the size distribution of the avalanches follows a power law. Power laws reflect complexity because they are similar on all scales. Suppose that the number n of avalanches of size s is described by the power law
![\[ n=as^ b, \]](http://plus.maths.org/MI/plus/latestnews/sep-dec08/managers/indexhtml4/images/img-0003.png) |
for some constants a and b. Now multiply s by a large number c, so you're now looking at large avalanches. These then follow the power law
![\[ n=ac^ bs^ b, \]](http://plus.maths.org/MI/plus/latestnews/sep-dec08/managers/indexhtml4/images/img-0007.png) |
which, apart from the constants involved, is essentially the same as that for smaller avalanches - the same type of behaviour occurs on all scales.
Given that the power law highlights the fact that there is something interesting going on, the researchers set out to find out what it was. What are the simple rules of football management that govern this system, and is there self-organised criticality?
 The model
The model
The authors constructed a model which includes a manager's reputation — this is either enhanced or diminished, depending on the result of each match. The core of the model is a round-robin tournament with 20 teams playing each other once at home and once away — just like in the Premier League. The probabilities of win, lose and draw were modelled as 37%, 26%, 37%, respectively — these probabilities are those observed in the English football league between the years 1881 and 1991 and are assumed to be independent of the managers involved.
The model starts with 20 randomly selected managers, each with a given reputation and tenure. (With a nod to realism, we will henceforth assume that all managers are male.) The initial reputation of each manager is described by a positive whole number, which is chosen at random from the numbers between the firing threshold and the poaching threshold (more on these in a moment). Each manager also starts with a random tenure length between 1 and 40 years. The managers gain reputation (+ 2 points in the model) every time their teams win, and lose reputation (-2 points) when their teams lose. There are no points for draws. Each game has equal importance and so each result is equally important for a manager's reputation.
The length of a manager's tenure depends on how his reputation evolves. Termination of tenure can occur for four reasons:
- The manager loses his job when his reputation falls below the firing threshold — that is, he is sacked;
- The manager is poached by another club when his reputation reaches the poaching threshold — that is, he gets a better deal;
- The manager retires if he gets too old (another parameter that can be varied);
- The manager's team is relegated to a lower league because it has the lowest reputation at the end of the season — the team is demoted out of the league.
When a manager leaves the system — that is, he is either fired or poached, relegated or retired — his place in the league is taken by another manager with tenure length of zero and a random starting reputation.
With these rules in place, the researchers ran many simulations, varying the random parameters in each run. Such a process is known as a Monte-Carlo simulation. They recorded the distribution of tenure lengths corresponding to one hundred years of competition. They found that for a very broad range of starting parameters, the model produced a tenure length distribution statistically indistinguishable from a power-law distribution. Similar results were obtained for different probability distributions of win, loss or draw. However, the researchers also found that power laws only emerge when a win enhances reputation by the same amount as it is decreased by a loss, and when each match has equal importance. The latter makes sense if you think that the aim of a Premier League team is to maximise its profit: you need to fill the stadiums and make as much advertising revenue as you can at each game. And as the Premier League is a first-past-the-post competition, each win has equal worth on the league table, with position on the table more than anything guaranteeing further advertising and merchandising returns.
Coming back to self-organised criticality, the researchers admit that their model does not prove the existence of this phenomenon in the world of sport. In fact, the model is not quite as self-organising as it could be, since certain parameters need to be artificially fixed at the outset. They do believe, however, that certain other factors point in the direction of self-organised criticality. The Premier League, they postulate, follows the Red Queen principle: it is an arms race where constant development is needed simply to compete. This explains why once a league has reached a self-organised critical state, it might stay there for a prolonged period of time. It is simply too difficult for a team to shake up the system, given that they are already in a process of continual change in order to stay with the pack. The term Red Queen comes from Lewis Carroll's Through the Looking-Glass in which the Red Queen says: "It takes all the running you can do, to keep in the same place".
What the results surprisingly show is that ability and talent, although obviously playing some role, do not play a major role in a manager's success. His survival is far more determined by the sacking and poaching thresholds and simple randomness in his team's results. 2007 Chelsea manager Avram Grant is a good example of this: as he started his tenure with a low reputation, despite his team's good results, probabilities took their toll and he was sacked at the end of the season.
In any case, it's hard to feel sorry for prematurely sacked Premier League managers when their average salaries are over £2 million.
For more info, see the following:
- The paper A power-law distribution for tenure lengths of sports managers has appeared in the journal Physica A;
- The Plus article Understanding uncertainty: The Premier League finds more randomness in the Premiere League;
- There is more about sand pile models in the Plus article Like sand through the hour glass;
- And about power laws in the Plus articles The mystery of Zipf, Network news, and Beating bird flu with bills.












I was searching the blogs for a long time and that is good to know that I have found such blogs here. Great working!https://thepartyparty.us/ Keep it up!
ReplyDeletevery nice blog i like it Hockey Factory Shop Discount codes content is very good
ReplyDeleteRecently I read your blog and it was very good. I'm really impressed with this blog. The content was really appreciating. Thanks for sharing this.
ReplyDeletepremier league highlights today
It’s great to come across a blog every once in a while that isn’t the same out of date rehashed material. Fantastic read. Best tips premier league service provider.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteAfter a long time, I read a very beautiful and very important article that I enjoyed reading. I have found that this article has many important points, I sincerely thank the admin of this website for sharing it. Best Ajax Third Jersey service provider.
ReplyDeleteThis means that you have equal chance of winning online or at the casino. 꽁머니 추천
ReplyDeleteThis is really very nice article.You have done very good work.
ReplyDeleteI like your blog ,it is full of knowledge and gain.keep it up.
Prima Cartoonizer Crack
Football Manager Crack
FileMenu Tools Crack
Artweaver Plus Crack
MakeUp Pilot Crack
Start Menu X PRO Crack
VMware Workstation Pro Crack
Infix PDF Editor Pro Crack
iMyfone Umate Pro Crack