
At the very heart of sport is a fierce battle in which the combatants strive to outwit and outplay each other. Each thrust is matched by a parry and in the end, there can only be one winner. The rules of each sport dictate how that winner is determined, and, whether it is football, tennis, golf or chess, it is those who perform best on the day who take home the glory.
But it's not easy to get to the all-important final. True sporting supremacy cannot be decided in a one-off winner-takes-all event. Indeed, many championships are specifically designed such that the ultimate winners are not decided by the results of single events but rather by accumulated results over time. It is easy to rank teams within structured leagues like the English Premiere League, as each team plays all opponents, so that eventually the best teams rise to the top. But it is not always that easy — indeed, more often than not, it is very difficult. Keeping with the football example, how can we compare international football teams such as Australia and England who very rarely play each other? International football sides do not play as often as club teams, so we can't have the same confidence that the team with the most wins over a year, or even the highest percentage of wins, is the best team in the world. And how can we determine which wins are the most important?
Different sports have developed their own way of dealing with the subtleties of ranking their players and teams, and this article is the first of a series looking at these ranking systems. In future instalments we'll be looking at rugby, football, cricket, tennis and golf, but to start off, we explore the ranking systems of two very different sports: chess and sumo wrestling.
Chess It should not surprise anyone that, of all sports, chess has the most mathematically elegant ranking system — it is, of course, a very cerebral pursuit. The ranking system, called the ELO system, was developed by Arpad Elo, a Hungarian-born American physics professor and chess guru.
Unlike in other sports such as tennis, where rating points can be awarded subjectively — for example, an important tennis tournament might be worth ten times more than another — Elo's idea was to mathematically estimate, based on observation, actual player ability.
 Elo's original assumption was that a player's performance varies from game to game in a way that can be described by the normal distribution: if you measure a player's skill numerically and then plot the number of times he or she has achieved at each skill value against the possible skill values, you will get a bell-shaped curve as shown in figure 1. The peak of the curve is the mean of the distribution and represents the player's true skill, while the tails represent untypically good or bad performances. So while a player can have very good and very bad days, on average they perform somewhere near their mean value. The aim of the ELO system is to estimate the mean value for each player by looking at how often they win, lose and draw against other players with different abilities — this gives you their rating. We can use the player ratings to predict the probability of one player beating another, and the smaller your chance of winning, the more rating points you get if you do win.
Elo's original assumption was that a player's performance varies from game to game in a way that can be described by the normal distribution: if you measure a player's skill numerically and then plot the number of times he or she has achieved at each skill value against the possible skill values, you will get a bell-shaped curve as shown in figure 1. The peak of the curve is the mean of the distribution and represents the player's true skill, while the tails represent untypically good or bad performances. So while a player can have very good and very bad days, on average they perform somewhere near their mean value. The aim of the ELO system is to estimate the mean value for each player by looking at how often they win, lose and draw against other players with different abilities — this gives you their rating. We can use the player ratings to predict the probability of one player beating another, and the smaller your chance of winning, the more rating points you get if you do win.
Elo's original model used normal distributions of player ability, however observations have shown that chess performance is probably not normally distributed — weaker players actually have a greater winning chance than Elo's original model predicted. Therefore, the modern ELO system is based on the logistic distribution which gives the lower rated player a greater, and more accurate, chance of winning.
To see how this system works in practice, let's have a closer look at the maths. Each player's ability is modelled as having a standard deviation of 200 rating points. The standard deviation is a measure of the spread of the data around the mean. In our case a low standard deviation would mean that the player's performance never strays far off the mean, while a high standard deviation means that he or she occasionally has pretty drastic off-days, both in the negative and positive sense. Traditionally in chess, ability categories like grand master, master and so on, spanned 200 rating points each, and this may be the reason why the value 200 was chosen for the standard deviation.
Based on these assumptions it's possible to work out the expected scores of a player  playing against player
playing against player  . If player
. If player  has a rating of
has a rating of  and player
and player  has a rating of
has a rating of  , the exact formula for the expected score of player
, the exact formula for the expected score of player  is
is
Similarly, the expected score for player  is
is
The following chart shows the probabilities involved in a game of chess based on Elo's original normal distribution, and the modified version employing the logistic model. The horizontal axis measures the difference between the rating of player A and player B and the vertical axis gives the chance of a win for player A. There is little difference between the two curves except in the tails, where the logistic curve gives the lower rated player a greater chance of winning.
Player ratings are updated at the end of each tournament. Imagine you are a player with rating 1784. In a tournament you play 5 games with the following results:
- Win against player rated 2314;
- Lose against player rated 1700;
- Draw against player rated 1302;
- Win against player rated 1492;
- Lose against player rated 1927.
As you had two wins and a draw, you scored 2.5. However, your expected score, as calculated from the above formula, was 0.045 + 0.619 + 0.941 + 0.843 + 0.306 = 2.754. Therefore you didn't do as well as was expected.
When a player’s tournament score is better than the expected score, the ELO system adjusts the player’s ranking upward. Similarly when a player’s tournament scores is less than the expected score, the rating is adjusted downward. Supposing player  was expected to score
was expected to score  points but actually scored
points but actually scored  points, their new rating
points, their new rating  is
is
where  is a constant which causes much debate in the chess world. Some chess tournaments use
is a constant which causes much debate in the chess world. Some chess tournaments use  for masters players and
for masters players and  for weaker players. This means that unusually good or bad performances weigh more heavily for weak players than they do for masters.
for weaker players. This means that unusually good or bad performances weigh more heavily for weak players than they do for masters.
For our player with rating 1784, the new rating becomes
As with all ranking systems, there are controversies surrounding the ELO system. These include
- Mixing: Like all ranking systems, the ELO system works best when players play often against many different people. Imagine a chess club whose members generally play among themselves. Their ratings therefore reflect how good each member is compared to their club's other members. But if that club then plays against a second club in a tournament, there is every chance that one of the clubs is considerably stronger than the other. This however will not be reflected in the ratings before competition. Only after some time will the ratings reflect player ability across both clubs rather than just within each club.
- Initial score: How should a new player be ranked, and how credible is that rank?
- The constant K: What is the right value of K? If K is too low, it is harder to win points, but if K is too high the system becomes too sensitive.
- Selective play: In order to maintain their rankings, players may selectively play weaker players.
- Time: How should a player who is not playing anymore, or plays infrequently, be ranked?
Sumo masters are decided in a way that's hard to quantify.
The ranking method of sumo wrestling is almost the complete opposite of chess — much like the sports themselves! Whilst some mathematics feeds into the ranking formulation, much of what determines a sumo's rank, especially in the upper ranks, cannot be quantified.
There are six divisions in sumo wrestling — makuuchi, juryo, makushita, sandanme, jonidan and jonokuchi. The top division, makuuchi, is very popular in Japan and has a complex inner ranking system, with yokozuna the ultimate rank. The following figure shows the breakdown of sumo ranks, with the numbers in brackets representing the number of wrestlers at that level.
Sumo wrestlers fight in tournaments called basho. These tournaments run to 15 days and depending on the division consist of seven or 15 bouts. Grand Sumo tournaments, known as honbasho, determine sumo rankings and there are six throughout the year. In these tournaments, the wrestlers fight within their divisions — sekitori fight 15 matches whilst the lower divisions fight seven. As there are more wrestlers than there are matches, sumo elders called oyakata determine the match-ups the day before.
 In general, rising to sekiwake, the third level of the highest division, requires that you win more bouts than you lose in tournaments. If you have a positive winning record in a tournament, you will move up, and vice versa. If your winning record is 13-2, you will climb higher than someone with an 8-7 record.
In general, rising to sekiwake, the third level of the highest division, requires that you win more bouts than you lose in tournaments. If you have a positive winning record in a tournament, you will move up, and vice versa. If your winning record is 13-2, you will climb higher than someone with an 8-7 record.
The jump from the third division, makushita, to the second division, juryo, is perhaps the most important rank distinction in sumo. Juryo is the first rank of sekitori, and the ultimate aim of most wrestlers. Wrestlers lower than this rank have to do chores for their superiors and are essentially sumo slaves. Non-sekitori wrestlers become tsukebito (personal valets) for the higher ranked wrestlers. Those at the very top of the table, yokozuna, typically have four tsukebito while everyone else in the sekitori class normally has two or three depending on prestige and seniority. There is probably no other sport in which the difference between ranks is so important — tsukebito need to accompany their superiors wherever they go, and while sekitori can relax and hang out with their fan clubs at the end of the day, or go home to their apartments, the junior wrestlers must clean the sumo stables and live in communal dormitories. The difference in salary is also huge — juryo rank receives a base salary of ¥1,036,000 (around £7,000) plus considerable add-ons and bonuses, while there is no salary below this rank.
Given this massive discrepancy, you can see why maintaining a rank of sekitori is very important for a sumo wrestler. Indeed, the ancient sport has recently been tainted by a match fixing controversy. A study by Steven Levitt and Mark Duggan in the book Freakonomics showed that 80% of wrestlers with 7-7 records win their matches at the end of tournaments, when you would expect this percentage to be closer to 50%. The authors conclude that those who already have 8 wins collude with those who are 7-7 and let them win, since they have already secured their ranking.
The rank of yokozuna is the highest and most venerable position in the sumo world. The yokozuna is the Grand Champion. Ozeki are also held in very high regard, and there are always at least two ozeki — there is no minimum on the number of yokozuna at any one time, however there may be none. There are currently two yokozuna.
To achieve these ranks, you must do more than have a positive honbasho record. By the time a wrestler reaches the rank of sekiwake, he has been able to maintain a positive honbasho record for some time. If a sekiwake starts to accumulate 10-5 or better records and occasionally upsets a yokozuna, the sumo administrative board (called the sumo kyokai) will consider a promotion to ozeki. One of the benefits of ozeki is that there is no automatic demotion based on match results — to be demoted back to sekiwake requires two consecutive losing streaks.
 If an ozeki starts winning honbasho, he may be judged by the promotion council (the yokozuna shingi iinkai) for possible further promotion. And here is where the real mysteries of sumo ranking come in. The promotion council can recommend the ozeki to the riji-kai (board of directors) of the sumo kyokai. The first thing they consider are the previous three honbasho. Out of those 45 bouts, 38 is the minimum number of wins needed to be considered and the ozeki should have won two consecutive tournaments — but this is not all! The wrestlers must show respect for the sumo kyokai's rule and tradition, and towards past wrestlers, and also possess a character and attitude appropriate for a yokozuna. They must have hinkaku (dignity and grace) and have mastered basic sumo techniques such as shiko (the way a sumo holds his foot aloft before pounded it into the ground) and suri-ashi (the technique of keeping the bottom of each foot always touching the ground while moving). Once the riji-kai approves the promotion, it needs to be finally decided by the banzuke hensei kaigi (ranking arranging committee).
If an ozeki starts winning honbasho, he may be judged by the promotion council (the yokozuna shingi iinkai) for possible further promotion. And here is where the real mysteries of sumo ranking come in. The promotion council can recommend the ozeki to the riji-kai (board of directors) of the sumo kyokai. The first thing they consider are the previous three honbasho. Out of those 45 bouts, 38 is the minimum number of wins needed to be considered and the ozeki should have won two consecutive tournaments — but this is not all! The wrestlers must show respect for the sumo kyokai's rule and tradition, and towards past wrestlers, and also possess a character and attitude appropriate for a yokozuna. They must have hinkaku (dignity and grace) and have mastered basic sumo techniques such as shiko (the way a sumo holds his foot aloft before pounded it into the ground) and suri-ashi (the technique of keeping the bottom of each foot always touching the ground while moving). Once the riji-kai approves the promotion, it needs to be finally decided by the banzuke hensei kaigi (ranking arranging committee).
Famously in 1991, Hawaiian-born Samoan wrestler Konishiki, the heaviest wrestler ever in top-flight sumo, was denied yokozuna even though he had won two championships in a row. The chairman of the promotion council said, "We wanted to make doubly sure that Konishiki is worthy to be a grand champion. Therefore, we decided to wait for another tournament." It was speculated at the time that a foreign-born sumo wrestler could never make yokozuna as they could not possess the required cultural understanding. Since then however, there have been foreign-born yokozuna.
A yokozuna cannot be demoted and is expected to retire if his performance starts to dip.
As you can see, mathematics hardly comes into sumo, rather the rankings are based on trust and veneration for those in charge. Most other sports, however, do require a more objective evaluation of their stars, and we'll have a look at some of them in future articles of this series.
For more, see Plus Magazine. For more on chess, see Chess rankings, ChessBase and Knowledgerush, and for Sumo see the Sumo FAQ.

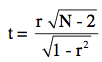








 Elo's original assumption was that a player's performance varies from game to game in a way that can be described by the normal distribution: if you
Elo's original assumption was that a player's performance varies from game to game in a way that can be described by the normal distribution: if you  playing against player
playing against player  . If player
. If player  and player
and player  , the exact formula for the expected score of player
, the exact formula for the expected score of player ![\[ E_ A = \frac{1}{1+10^{\frac{R_ B-R_ A}{400}}}. \]](http://plus.maths.org/MI/plus/latestnews/may-aug09/chessumo/indexhtml1/images/img-0005.png)
![\[ E_ B = \frac{1}{1+10^{\frac{R_ A-R_ B}{400}}}. \]](http://plus.maths.org/MI/plus/latestnews/may-aug09/chessumo/indexhtml1/images/img-0007.png)

 was expected to score
was expected to score  points but actually scored
points but actually scored  points, their new rating
points, their new rating  is
is ![\[ R^\prime _ A=R_ A + K (S_ A - E_ A), \]](http://plus.maths.org/MI/plus/latestnews/may-aug09/chessumo/indexhtml2/images/img-0005.png)
 is a constant which causes much debate in the chess world. Some chess tournaments use
is a constant which causes much debate in the chess world. Some chess tournaments use  for masters players and
for masters players and  for weaker players. This means that unusually good or bad performances weigh more heavily for weak players than they do for masters.
for weaker players. This means that unusually good or bad performances weigh more heavily for weak players than they do for masters.![\[ R^\prime _ A = 1784 + 32(2.5-2.754) = 1776. \]](http://plus.maths.org/MI/plus/latestnews/may-aug09/chessumo/indexhtml3/images/img-0002.png)















