The 2012 Olympics are now only days away. I put together this article for Plus Magazine - check out the original article on Plus for full coverage, and follow Plus closely during the Olympics as they will be running regular sporting articles - see their package on maths and sport.
The 2012 Olympics are now only days away. I put together this article for Plus Magazine - check out the original article on Plus for full coverage, and follow Plus closely during the Olympics as they will be running regular sporting articles - see their package on maths and sport.
The men's and women's 100 metre freestyle swimming races are set to
be two of the most glamorous events of the London 2012 Olympic Games.
Much has been made of the swimming events for London 2012 because the
previous 2008 Beijing Olympics saw an unprecedented number of new world
records, due to the use of controversial swimsuits. Sixty-six Olympic
records were broken during the 2008 Games – indeed, in some races the
first five finishers beat the old Olympic mark – and 70 world swimming
records were broken in total throughout the year 2008.
The controversial swimsuits have now been banned, but the records
they set have not been revoked, so the 2012 Olympics are unlikely to see
many new records. This does not mean, however, that the events will be
any less competitive, and indeed if records are broken, the performances
will likely be exceptional.
Pumping iron or beating drag?
Broadly speaking, records in all sports are determined by two
factors: the physical and mental performance of the athlete and
technological influence. Pure physical performance tends to improve over time as our understanding of the scientific aspects of sport lead to
improved training techniques, diets and race tactics. Technological
factors, such as a more supportive shoe, aerodynamic bike or faster car
can also lead to quicker times. Some sports such as Formula One car
racing have an obvious reliance on technology – notwithstanding the
incredible physical and mental toughness required to withstand the
cockpit of the F1 car. Other sports such as long distance running may
have very little to do with technology, with famous examples of Kenyan
runners winning major world events bare foot.
Although at first impression swimming seems to rely little on
technology, there are many factors outside a swimmer's control that
influence their final time. The type of pool has a considerable
influence — the first four Olympics Games were not held in pools, but
in open water (1896 in the Mediterranean Sea, 1900 in the Seine River,
1904 in an artificial lake). The 1908 Games were held in a 100 metre
pool, whilst the 1912 Games were held in Stockholm harbour. The 1924
Olympics were the first to use a 50 metre pool with marked lanes, and
the 1936 Games saw the introduction of diving blocks. Before the 1940s
male swimmers wore full body suits that were heavy and caused a lot of
drag. Pool designs have also changed with pool and lane width modified
to eliminate currents, and energy absorbing lane barriers used to stop
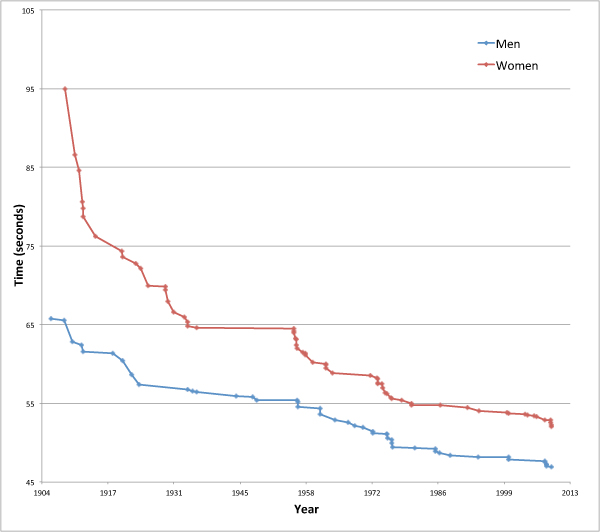
waves from adjacent lanes. (See below for a chart of world records over the 100 metre freestyle event since 1904.)
There are, broadly speaking, two things you can do to reduce your swimming time:
-
Increase your power
-
Reduce your drag
The magnitude
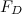
of the drag force acting on a swimmer moving in a fluid is given by the following equation
where
-
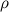 is the mass density of the fluid
is the mass density of the fluid
-
 is the speed of the swimmer relative to the fluid
is the speed of the swimmer relative to the fluid
-
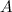 is the swimmer's cross-sectional area, that is the area of your body as it is pushing through the water head on
is the swimmer's cross-sectional area, that is the area of your body as it is pushing through the water head on
-
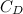 is the drag-coefficient,
a number which depends on factors such as the exact shape of the
swimmer and the hydrodynamic qualities of their skin and what they are
wearing.
is the drag-coefficient,
a number which depends on factors such as the exact shape of the
swimmer and the hydrodynamic qualities of their skin and what they are
wearing.
Although it may seem like going to the gym and pumping some iron
might be the obvious thing to do, reducing your drag is actually a
speedier route to a quick lap time. Your
power 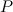
is
the rate at which your body uses its energy, and when you are swimming
the power you exert is proportional to the cube of your speed

Now suppose you want to increase your speed by 10%, from

to
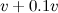
. To do this solely by increasing your power, you need to exert a new power
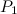
The percentage increase in the power required is given by
Since
we have
So to increase your speed by 10% solely by increasing your power, you need to increase the power by 33.1%.
Reducing your drag is easier. From the equation for power above we see that the drag coefficient
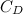
is
Keeping your power output and cross-sectional area the same, increasing your speed by 10% requires a new drag coefficient
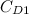
of
The percentage decrease in drag coefficient is given by
So the 10% increase in speed requires a 25% reduction in the drag coefficient.
The exact same working can be used for cross-sectional area — a
reduction of 25% will increase your speed by 10%. This is actually the
key to the simplest method of reducing drag for most swimmers: improving
your technique. Because human lungs are full of air, when we swim our
upper body tends to rise and our lower body sinks, increasing
cross-sectional area
A. The drag force increases and you slow
down. Keeping your feet nearer the surface is the easiest method of
reducing drag for everyday swimmers.
Drugless doping
At the top end of competitive swimming nearly all swimmers already
have very good techniques, so swimsuit technology comes into play.
Materials have been developed that increase the swimmer's buoyancy,
making it easier to keep their feet near the surface, and reduce the
drag coefficient as the material glides through the water more easily
than human skin does.
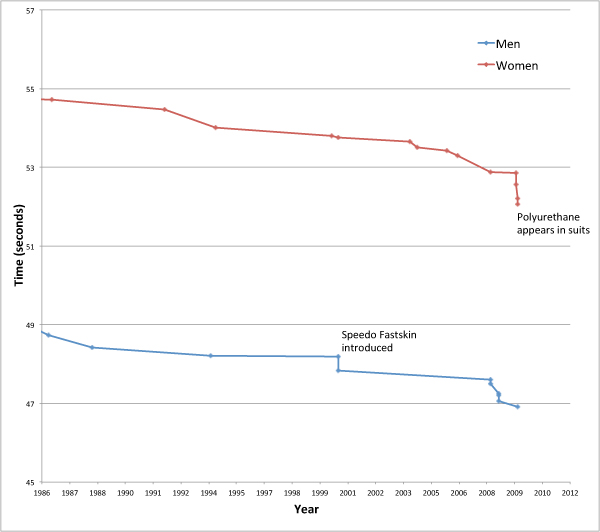
Full-length high-tech swimsuits were first introduced in 1999 before the 2000 Sydney Olympics, with the
Speedo Fastskin suits containing V-shaped ridges, modelled on shark skin, to reduce drag. By 2008, the
Speedo LZR Racer
swimsuit was the most advanced. It was put through wind tunnel tests by
NASA and mathematicians modelled water flow around it using a technique
called
computational fluid dynamics, which simulates how fluid flows around objects (see
this article
for more on modelling fluid flow). And this research all happened
before real swimmers tested the suits in real pools. In Beijing, 89% of
all swimming medals were won by swimmers wearing
LZR Racer suits.
One of the ways the
LZR Racer suits reduce drag is by having
panels of a plastic called polyurethane on parts of the body that
produce the highest drag. Other swimsuit manufacturers took note.
Instead of being textile based with only patches of polyurethane, suits
like the subsequent
Arena X-Glide were made entirely of
polyurethane. These suits were completely impermeable to water, so
swimmers could conceivably complete their race without getting wet
between their ankles and neck! Records continued to tumble. See more on the Speedo swimsuit technology in
this article.
The governing body for swimming,
FINA
(Fédération Internationale de Natation – International Swimming
Federation), took note of the plummeting records and the accusations of
"technological doping". In March 2009 it put limits on the suits'
thickness and buoyancy, affirming that "FINA wishes to recall the main
and core principle that swimming is a sport essentially based on the
physical performance of the athlete." They also stipulated that the
suits should not cover the neck, shoulders and ankles.
This edict did not actually ban any of the new suits at the 2009
World Aquatics Championships (the "plastic games") — 38 meet records
were broken. Subsequently all body-length swimsuits were banned. It was
ruled that men's swimsuits may only cover the area from the waist to
the knee, and women's from the shoulder to the knee. FINA also ruled
that the fabric used must be a textile and not polyurethane. Despite
these new rules, the records set by the now banned swimsuits were not
revoked and still stand.
And as the term "textile" is not defined, and as scientists are
pretty clever folk, the ambiguity of the new rules leaves open a large
area for swimsuit development.
Record history
The progression of world records over the 100 metre freestyle event
is shown below. Apart from some of the pool changes mentioned earlier,
records have continued to drop as we increase our understanding of our
physical abilities. Other innovations which have helped reduce times
include the introduction of diving blocks in 1936 – previously swimmers
had just dived from the wall – and the development of the
tumble turn in the 1950s.
It is interesting to note that freestyle as we know it now has not
always existed. By definition, in freestyle races you can pretty much
swim however you like (with some exceptions), unlike breaststroke,
butterfly or backstroke which have defined methods of swimming. During
the 1840s, even though they were beaten by native North Americans
swimming with a front crawl style, British gentleman swimmers (in an oh
so British fashion) swam only breaststroke, considering the front crawl
too splashy, barbaric and un-European. In the late 1800s, the quickest
(British) freestyle was the
Trudgen style, named after John
Arthur Trudgen, whose stroke was a combination of side stroke and front
crawl. The Australian Dick Cavill modified this style to something
similar to what is seen today with his
Australian crawl and set a new world record for 100 yards in 1902.
The figure below shows a close-up of times from the early 1980s. You
can see the decline around 1999 when the first fast-suits came in, then
the sharp decline in 2008. It is difficult to predict when the next dots
on the curves will occur.
At the time of writing, Australians are the favourites for both the
men's and women's 100 metre freestyle events, with James Magnussen and
Matt Targett having recorded the quickest men's 100 metre times in 2012,
and Melanie Schlanger the quickest women's time. The UK's Francesca
Halsall is 5th so far this year in the women's event, however Simon
Burnett in 39th would be doing well to make it past the heats in the
men's.



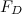 of the drag force acting on a swimmer moving in a fluid is given by the following equation
of the drag force acting on a swimmer moving in a fluid is given by the following equation![\[ F_ D=\frac{1}{2}\rho v^2 C_ D A, \]](http://plus.maths.org/MI/1090f42a51914e0ebd03b208305002ac/images/img-0002.png)
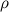 is the mass density of the fluid
is the mass density of the fluid is the speed of the swimmer relative to the fluid
is the speed of the swimmer relative to the fluid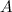 is the swimmer's cross-sectional area, that is the area of your body as it is pushing through the water head on
is the swimmer's cross-sectional area, that is the area of your body as it is pushing through the water head on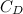 is the drag-coefficient,
a number which depends on factors such as the exact shape of the
swimmer and the hydrodynamic qualities of their skin and what they are
wearing.
is the drag-coefficient,
a number which depends on factors such as the exact shape of the
swimmer and the hydrodynamic qualities of their skin and what they are
wearing.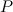 is
the rate at which your body uses its energy, and when you are swimming
the power you exert is proportional to the cube of your speed
is
the rate at which your body uses its energy, and when you are swimming
the power you exert is proportional to the cube of your speed 
![\[ P=F_ D v = \frac{1}{2}\rho C_ D A v^3. \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0003.png)
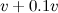 . To do this solely by increasing your power, you need to exert a new power
. To do this solely by increasing your power, you need to exert a new power 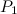
![\[ P_1 = \frac{1}{2}\rho C_ D A (v+0.1v)^3. \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0006.png)
![\[ Increase = 100 \times \frac{P_1-P}{P}= 100 \times (\frac{P_1}{P}-1). \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0007.png)
![\[ \frac{P_1}{P} = \frac{\frac{1}{2}\rho C_ D A (v+0.1v)^3}{\frac{1}{2}\rho C_ D A v^3}=(1.1)^3=1.331 \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0008.png)
![\[ Increase =100 \times (1.331-1)\% =33.1\% . \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0009.png)
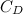 is
is![\[ C_ D=\frac{2P}{\rho A v^3}. \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0011.png)
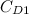 of
of![\[ C_{D1}=\frac{2P}{\rho A (v+0.1v)^3}. \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0013.png)
![\[ Decrease = 100 \times \frac{C_ D-C_{D1}}{C_ D}=100 \times (1-\frac{C_{D1}}{C_ D}) = 100 \times (1-\frac{1}{1.1^3})= 25\% . \]](http://plus.maths.org/MI/caa263a0adba65e63c48c3c9203b58b5/images/img-0014.png)