
The popularity of
Triple J's annual Hottest 100 has made my wonder what my favourite songs of all time are and whether I could come up with a list based on some actual data. The information I have to use is my
iTunes data since 2005. Being only 8 years of my life, this data set is limited. But with any luck (that is, if the assumptions hold true) the following algorithms will stay appropriate into the future and require only minor tweaking. What we're trying to do is come up with a method that will tell me, from my listening habits in
iTunes, what my favourite songs are. Whether you actually listen to your favourite songs more than others is a debate for another time.
iTunes doesn't tell you when songs were played, just how many times, so the useful parameters we can export for each song are "Play Count" (
p) and "Date Added". If we add up all the individual play counts, we get the "Total Play Count" for the entire collection (
P). Date Added can be turned into the number of days the song has been in the collection - time (
t). We also know the number of songs in the collection now (
N) and at various times in the past when I've exported the data.
First cut:
An easy first-cut model is to simply divide each song's play count by its time in the collection and order the songs by this rate of play. As a first attempt this may seem logical, however the problem is that it is heavily biased towards newer songs. You're likely to listen to a song a few times after you add it before it slips back into your various playlists. It also doesn't take into account that there are more songs in the collection now than at the start.
What we need to do is come up with an equation that tells us how many
times a song is expected to have been played depending on when it was
added. We can then compare this number to how many times it was actually
played and order the songs by this ratio.
Second cut:
}=\frac{A}{Bt+N_0})
This second version suffers from the same biasing problem as the first, but does take into account that the number of songs in the collection is changing over time. This is important as if you assume that you listen to music for about the same amount of time each day, then the more songs you have in your collection, the less likely you are to randomly hear the same song twice. Hence, songs that are played regularly when the collection is small should not be treated in the same way as songs played with the same frequency when the collection is large.
N0 is the number of songs in the collection at
t0. This model assumes that the number of songs in the collection grows linearly over time (
A and
B are constants) - that is, the same number of songs are added each month. This is about right for my collection. The integration is left as an exercise for the reader (hint, you get a log function).
Third cut:
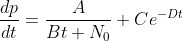
This final version takes into account that when you add new songs to your collection that you like, you are likely to listen to them quite a lot, independently of the number of songs that are already there - that is, they get added to a "new songs" playlist. The novelty of a new song eventually wears off, so the way we've modelled this is to use an exponential factor. You can tweek the coefficients (
C and
D) by thinking about the "half life" of a new song. The integration is left as an exercise for the reader (hint, you get a log function and an exponential).
The equation now contains two components - the first modelling the number of plays expected through random play and the second the impact of adding new songs to the collection. The model suggests that I play the same number of songs each year (apart from a barely perceptible increase due to the exponential factor) and it seems to work pretty well. This model won't work if and when I swap over
to streaming music, as opposed to owning it, as my major form of music
consumption, but for now it's holding up. Having played around with the coefficients, the list as it stands is below. It pretty much represents upbeat songs I go running with and songs my 2-year old likes - for whatever reason, he likes Korean pop music! I have to think that the novelty of Psy will wear off over time, but Hall and Oates, they'll never die.
| Gangnam Style |
PSY |
|
| I Remember |
Deadmau5 and Kaskade |
|
| ABC News Theme Remix |
Pendulum |
|
| You Make My Dreams |
Hall & Oates |
|
| Shooting Stars |
Bag Raiders |
|
| This Boy's In Love |
The Presets |
|
| Get Shaky |
Ian Carey Project |
|
| Monster |
BIGBANG |
|
| From Above |
Ben Folds |
|
| Banquet |
Bloc Party |
|




















